Description
训练模型时,很容易就会陷入 overfit 的问题中。如下图所示,
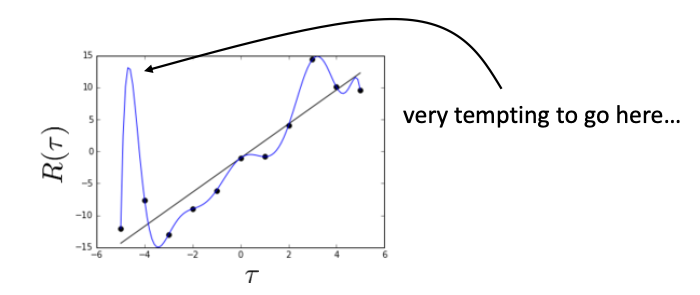
真正的轨迹应该是黑色线条,我们用数据预测出来的模型是蓝色线条。 可以看出来,有些地方的奖励预测过高,导致会在某些地方的选择与正确动作相差巨大。
假设我们有一个关于模型准确率的函数,用来描述模型在当前状态下的预测的准确率。 下图蓝色部分为 95% 的置信区间,它表示,模型有 95% 的概率确定下一个状态会在蓝色区间内, 但模型无法知道到底在蓝色区间内的什么地方。
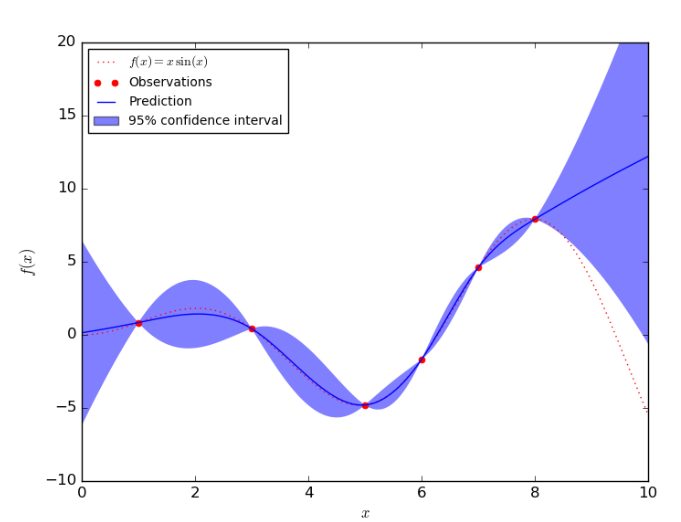
模型不确定性
Idea 1. 计算输出动作的交叉熵。熵越高,模型越不稳定。
这种想法是不可行的。下图中蓝线表示生成的模型,可以看出,模型的方差基本上为 0,即模型输出的熵为 0, 但这个模型是非常不稳定的。 “Model is certain about the data, but we are not certain about the model.”
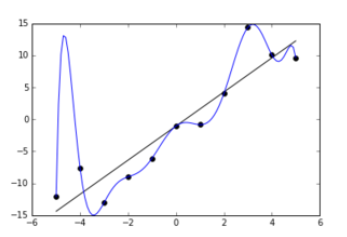
模型的不确定性其实体现在两个方面,一是数据的不确定性,二是模型本身的不确定性。 计算交叉熵解决的只是数据的不确定性。
Idea 2. 计算模型本身的不确定性
我们希望生成的模型可以满足这个条件:
也就是说,模型参数可以通过数据生成,数据也可以使用模型参数来生成。
其实, 就是说明模型不确定性的因素,它表示用这些数据生成一参数为 的模型的概率是多少。 然后将模型不确定性和数据不确定性结合起来: