Consensus in Networked Multi-Agent Systems with Adversaries

Views

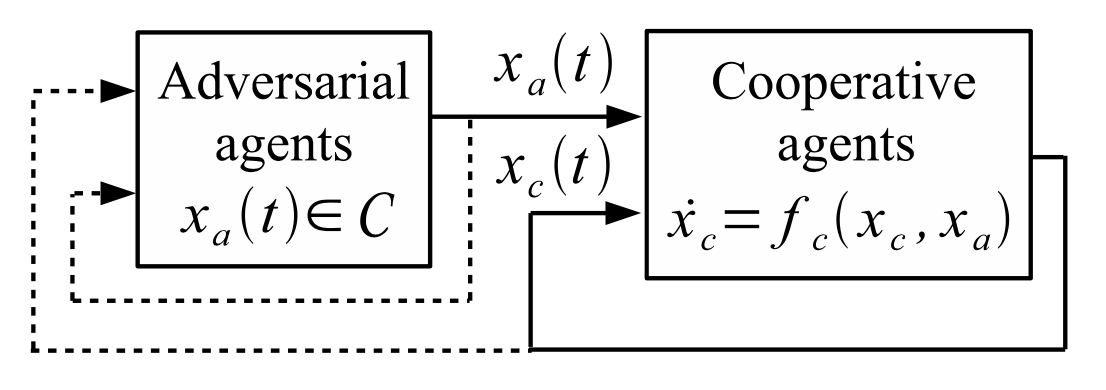
In the figure, $x_c=[x_1,\dots ,x_p{]}^T\in {\mathbb{R}}^p$ represents the states of the cooperative agents. Similarly, $x_a=[x_{p+1},\dots ,x+n]$ represents the states of the adversaries. The state feedback to the adversarial agents is shown as dashed lines to indicates that this information may or may not be used to influence the behavior of the adversaries. On the other hand, the cooperative agents must use the state information from all the agents in a similar manner since the cooperative agents are unaware of which agents are adversaries.

1. Cooperative Agents

   $$\dot{x_c}=f_c(x_c,x_a),x_c(0)=x_{c0},x_a(t)\in \mathbf{C}$$

   where $f_c(x_c,x_a)=[f_1(x_c,x_a)\dots f_p(x_c,x_a)]$

   Each cooperative agent i is designed in such a way so that the cooperative agents reach consensus in spite of the influence of at most F adversaries.

2. Adversarial Agents The adversarial agents are assumed to be designed for the purpose of disrupting the objective of the cooperative agents. The main limitation on the behavior of the adversaries is that the state trajectory of each agent is restricted to bounded continuous funcations of time .

Adversarial Agreement Problem

Consider a networked multi-agent system consisting of n agents. Assume there exists an upper bound F on the number of such agents. Then the adversarial agreement problem is defined by two conditions: agreement and validity.

The agreement condition states that the pairwise absolute difference between the states of the cooperative agents approaches zero asymptotically, regardless of the adversaries’ trajectories.

The validity condition states that the limit of the state trajectory of each cooperative agent exists and is contained in the interval formed by the initial states of cooperative agents, regardless of the adversaries’ trajectories.

Methods

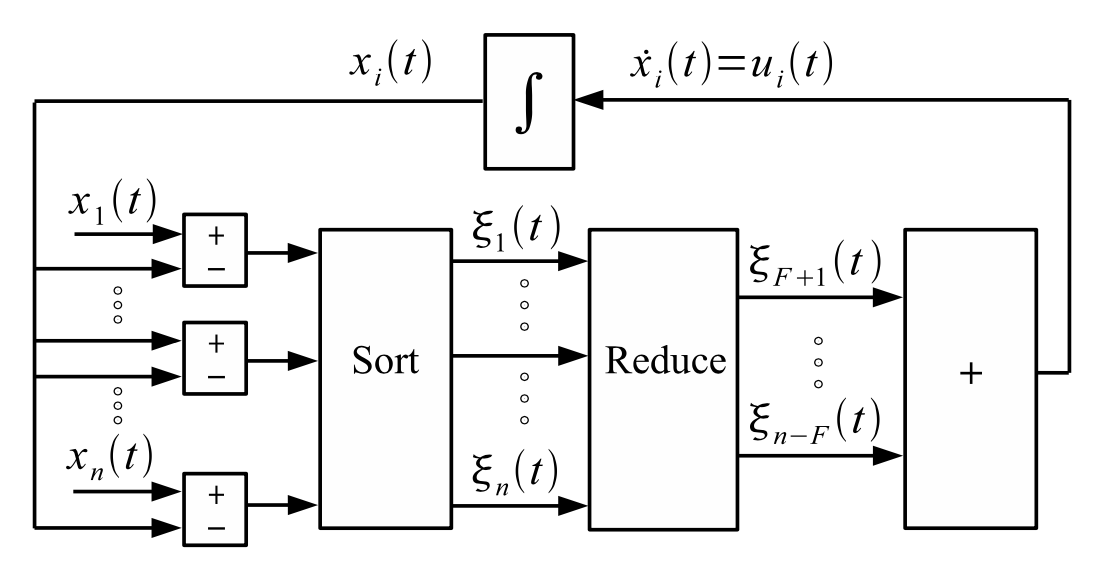
The Adversarially Robust Consensus Protocol(ARC-P), which is robust to adversaries in complete networks whenever there are more cooperative agents than adversaries.

The main idea of the protocol is for each agent to sort the state values and then filter(remove) the F largest and F smallest values so that the remaining values lie within the range of cooperative states. The state of the given agent i is then subtracted from each of the remaining values to form $m=n-2F$ relative state values. The relative state value is negative if the state of agent i is greater than the filtered state value and nonnegative otherwise.

Limitation

1. Complete graph
2. require condition: $n>2F$