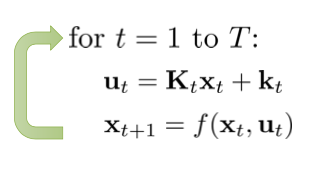Linear Quadratic Regression

Description

一般来说，强化学习很少有问题可以使用导数来求解，因为我们无法知道它的状态转移方程（环境动力学函数）， 比如在玩 Atari 游戏的时候，下一状态我们是无法通过公式定义来得到的。 假设我们现在知道状态转移方程，那么要如何通过导数来求得最优解呢？

先来考虑一下确定性环境。我们的目标是：

$$\underset{{\mathbf{u}}_1,\dots ,{\mathbf{u}}_T}{\min }\sum _{t=1}^{T}c\left({\mathbf{x}}_t,{\mathbf{u}}_t\right)\text{ s.t. }{\mathbf{x}}_t=f\left({\mathbf{x}}_{t-1},{\mathbf{u}}_{t-1}\right)$$

这是一个约束问题，我们可以把它转换为非约束问题：

$$\underset{{\mathbf{u}}_1,\dots ,{\mathbf{u}}_T}{\min }c\left({\mathbf{x}}_1,{\mathbf{u}}_1\right)+c\left(f\left({\mathbf{x}}_1,{\mathbf{u}}_1\right),{\mathbf{u}}_2\right)+\cdots +c\left(f(f(\dots )\dots ),{\mathbf{u}}_T\right)$$

对于非约束最优化问题，我们可以求导，使用梯度下降相关的方法来解决，需要计算

$$\frac{df}{d{\mathbf{x}}_t},\frac{df}{d{\mathbf{u}}_t},\frac{dc}{d{\mathbf{x}}_t},\frac{dc}{d{\mathbf{u}}_t}$$

求解上诉优化问题的两种方法又被称为 Shooting Methods I 和 Collocation Method 。

我们先使用 Shooting method 求解。 目标是：

$$\underset{{\mathbf{u}}_1,\dots ,{\mathbf{u}}_T}{\min }c\left({\mathbf{x}}_1,{\mathbf{u}}_1\right)+c\left(f\left({\mathbf{x}}_1,{\mathbf{u}}_1\right),{\mathbf{u}}_2\right)+\cdots +c\left(f(f(\dots )\dots ),{\mathbf{u}}_T\right)$$

其中：

f\left(\mathbf{x}_{t}, \mathbf{u}_{t}\right)=\mathbf{F}_{t}\left[\begin{array}{c} \mathbf{x}_{t} \\\\ \mathbf{u}_{t} \end{array}\right]+\mathbf{f}_{t} $$ ，线性函数，$F$ 为环境动力学相关的函数；

c\left(\mathbf{x}{t}, \mathbf{u}{t}\right)=\frac{1}{2}\left[\begin{array}{c} \mathbf{x}{t} \\ \mathbf{u}{t} \end{array}\right]^{T} \mathbf{C}{t}\left[\begin{array}{c} \mathbf{x}{t} \\ \mathbf{u}{t} \end{array}\right]+\left[\begin{array}{c} \mathbf{x}{t} \\ \mathbf{u}{t} \end{array}\right]^{T} \mathbf{c}{t} $$ ，二次函数，$C$ 为任意维度匹配的矩阵。

目标方程只对动作 $u_t$ 求导，且上一时刻的状态和动作会影响下一时刻的状态 （$x_t=f(x_{t-1},u_{t-1})$），进而影响下一时刻的损失 c 。 因此，我们需要使用反向传播的方法，把梯度从最后一个状态开始，传回第一个状态。

因此先计算对 $u_T$ 的求导： 最后一步执行后的损失为：（因为损失与状态和动作相关，所以使用 Q 来表示）

$$Q\left({\mathbf{x}}_T,{\mathbf{u}}_T\right)=\text{ const }+\frac{1}{2}{\left[\begin{array}{c}{\mathbf{x}}_T\\ \\ {\mathbf{u}}_T\end{array}\right]}^T{\mathbf{C}}_T\left[\begin{array}{c}{\mathbf{x}}_T\\ \\ {\mathbf{u}}_T\end{array}\right]+{\left[\begin{array}{c}{\mathbf{x}}_T\\ \\ {\mathbf{u}}_T\end{array}\right]}^T{\mathbf{c}}_T$$

设：

$${\mathbf{C}}_T=\left[\begin{array}{cc}{\mathbf{C}}_{{\mathbf{x}}_T,{\mathbf{x}}_T}& {\mathbf{C}}_{{\mathbf{x}}_T,{\mathbf{u}}_T}\\ & \\ {\mathbf{C}}_{{\mathbf{u}}_T,{\mathbf{x}}_T}& {\mathbf{C}}_{{\mathbf{u}}_T,{\mathbf{u}}_T}\end{array}\right]$$ $${\mathbf{c}}_T=\left[\begin{array}{l}{\mathbf{c}}_{{\mathbf{x}}_T}\\ \\ {\mathbf{c}}_{{\mathbf{u}}_T}\end{array}\right]$$

对 $u_T$ 求导：

\begin{array}{c} \nabla_{\mathbf{u}_{T}} Q\left(\mathbf{x}_{T}, \mathbf{u}_{T}\right)=\mathbf{C}_{\mathbf{u}_{T}, \mathbf{x}_{T}} \mathbf{x}_{T}+\mathbf{C}_{\mathbf{u}_{T}, \mathbf{u}_{T}} \mathbf{u}_{T}+\mathbf{c}_{\mathbf{u}_{T}}^{T}=0 \\ \mathbf{u}_{T}=-\mathbf{C}_{\mathbf{u}_{T}, \mathbf{u}_{T}}^{-1}\left(\mathbf{C}_{\mathbf{u}_{T}, \mathbf{x}_{T}} \mathbf{x}_{T}+\mathbf{c}_{\mathbf{u}_{T}}\right) \end{array}

化简：

\begin{array}{l} \mathbf{u}_{T}=\mathbf{K}_{T} \mathbf{x}_{T}+\mathbf{k}_{T} \\ \mathbf{K}_{T}=-\mathbf{C}_{\mathbf{u}_{T}, \mathbf{u}_{T}}^{-1} \mathbf{C}_{\mathbf{u}_{T}, \mathbf{x}_{T}} \\ \mathbf{k}_{T}=-\mathbf{C}_{\mathbf{u}_{T}, \mathbf{u}_{T}}^{-1} \mathbf{c}_{\mathbf{u}_{T}} \end{array}

可以看到，动作可以由状态来确定，因此损失可以只用状态来表示（V）：

$$V\left({\mathbf{x}}_T\right)=\mathrm{const}+\frac{1}{2}{\left[\begin{array}{c}{\mathbf{x}}_T\\ \\ {\mathbf{K}}_T{\mathbf{x}}_T+{\mathbf{k}}_T\end{array}\right]}^T{\mathbf{C}}_T\left[\begin{array}{c}{\mathbf{x}}_T\\ \\ {\mathbf{K}}_T{\mathbf{x}}_T+{\mathbf{k}}_T\end{array}\right]+{\left[\begin{array}{c}{\mathbf{x}}_T\\ \\ {\mathbf{K}}_T{\mathbf{x}}_T+{\mathbf{k}}_T\end{array}\right]}^T{\mathbf{c}}_T$$

展开：

\begin{aligned} V\left(\mathbf{x}_{T}\right)=& \frac{1}{2} \mathbf{x}_{T}^{T} \mathbf{C}_{\mathbf{x}_{T}, \mathbf{x}_{T}} \mathbf{x}_{T}+\frac{1}{2} \mathbf{x}_{T}^{T} \mathbf{C}_{\mathbf{x}_{T}, \mathbf{u}_{T}} \mathbf{K}_{T} \mathbf{x}_{T}+\frac{1}{2} \mathbf{x}_{T}^{T} \mathbf{K}_{T}^{T} \mathbf{C}_{\mathbf{u}_{T}, \mathbf{x}_{T}} \mathbf{x}_{T}+\frac{1}{2} \mathbf{x}_{T}^{T} \mathbf{K}_{T}^{T} \mathbf{C}_{\mathbf{u}_{T}, \mathbf{u}_{T}} \mathbf{K}_{T} \mathbf{x}_{T}+\\ & \mathbf{x}_{T}^{T} \mathbf{K}_{T}^{T} \mathbf{C}_{\mathbf{u}_{T}, \mathbf{u}_{T}} \mathbf{k}_{T}+\frac{1}{2} \mathbf{x}_{T}^{T} \mathbf{C}_{\mathbf{x}_{T}, \mathbf{u}_{T}} \mathbf{k}_{T}+\mathbf{x}_{T}^{T} \mathbf{c}_{\mathbf{x}_{T}}+\mathbf{x}_{T}^{T} \mathbf{K}_{T}^{T} \mathbf{c}_{\mathbf{u}_{T}}+\mathrm{const} \end{aligned}

化简：

\begin{array}{l} V\left(\mathbf{x}_{T}\right)=\mathrm{const}+\frac{1}{2} \mathbf{x}_{T}^{T} \mathbf{V}_{T} \mathbf{x}_{T}+\mathbf{x}_{T}^{T} \mathbf{v}_{T} \\ \mathbf{V}_{T}=\mathbf{C}_{\mathbf{x}_{T}, \mathbf{x}_{T}}+\mathbf{C}_{\mathbf{x}_{T}, \mathbf{u}_{T}} \mathbf{K}_{T}+\mathbf{K}_{T}^{T} \mathbf{C}_{\mathbf{u}_{T}, \mathbf{x}_{T}}+\mathbf{K}_{T}^{T} \mathbf{C}_{\mathbf{u}_{T}, \mathbf{u}_{T}} \mathbf{K}_{T} \\ \mathbf{v}_{T}=\mathbf{c}_{\mathbf{x}_{T}}+\mathbf{C}_{\mathbf{x}_{T}, \mathbf{u}_{T}} \mathbf{k}_{T}+\mathbf{K}_{T}^{T} \mathbf{C}_{\mathbf{u}_{T}}+\mathbf{K}_{T}^{T} \mathbf{C}_{\mathbf{u}_{T}, \mathbf{u}_{T}} \mathbf{k}_{T} \end{array}

接下来就可以计算目标函数对 $u_{T-1}$ 的求导了。方法和之前相同，只不过这一步的损失要加上最后一步的损失， 因为这一步的状态和动作会影响下一步的损失。

当前步的损失（Q）：

$$Q\left({\mathbf{x}}_{T-1},{\mathbf{u}}_{T-1}\right)=\mathrm{const}+\frac{1}{2}{\left[\begin{array}{c}{\mathbf{x}}_{T-1}\\ \\ {\mathbf{u}}_{T-1}\end{array}\right]}^T{\mathbf{C}}_{T-1}\left[\begin{array}{c}{\mathbf{x}}_{T-1}\\ \\ {\mathbf{u}}_{T-1}\end{array}\right]+{\left[\begin{array}{c}{\mathbf{x}}_{T-1}\\ \\ {\mathbf{u}}_{T-1}\end{array}\right]}^T{\mathbf{c}}_{T-1}+V\left(f\left({\mathbf{x}}_{T-1},{\mathbf{u}}_{T-1}\right)\right)$$

V:

$$V\left({\mathbf{x}}_T\right)=\mathrm{const}+\frac{1}{2}{\left[\begin{array}{c}{\mathbf{x}}_{T-1}\\ \\ {\mathbf{u}}_{T-1}\end{array}\right]}^T{\mathbf{F}}_{T-1}^T{\mathbf{V}}_T{\mathbf{F}}_{T-1}\left[\begin{array}{c}{\mathbf{x}}_{T-1}\\ \\ {\mathbf{u}}_{T-1}\end{array}\right]+{\left[\begin{array}{c}{\mathbf{x}}_{T-1}\\ \\ {\mathbf{u}}_{T-1}\end{array}\right]}^T{\mathbf{F}}_{T-1}^T{\mathbf{V}}_T{\mathbf{f}}_{T-1}+{\left[\begin{array}{c}{\mathbf{x}}_{T-1}\\ \\ {\mathbf{u}}_{T-1}\end{array}\right]}^T{\mathbf{F}}_{T-1}^T{\mathbf{v}}_T$$

合并上诉两项：

$$Q\left({\mathbf{x}}_{T-1},{\mathbf{u}}_{T-1}\right)=\text{ const }+\frac{1}{2}{\left[\begin{array}{c}{\mathbf{x}}_{T-1}\\ \\ {\mathbf{u}}_{T-1}\end{array}\right]}^T{\mathbf{Q}}_{T-1}\left[\begin{array}{c}{\mathbf{x}}_{T-1}\\ \\ {\mathbf{u}}_{T-1}\end{array}\right]+{\left[\begin{array}{c}{\mathbf{x}}_{T-1}\\ \\ {\mathbf{u}}_{T-1}\end{array}\right]}^T{\mathbf{q}}_{T-1}$$

其中：

\begin{array}{l} \mathbf{Q}_{T-1}=\mathbf{C}_{T-1}+\mathbf{F}_{T-1}^{T} \mathbf{V}_{T} \mathbf{F}_{T-1} \\ \mathbf{q}_{T-1}=\mathbf{c}_{T-1}+\mathbf{F}_{T-1}^{T} \mathbf{V}_{T} \mathbf{f}_{T-1}+\mathbf{F}_{T-1}^{T} \mathbf{v}_{T} \end{array}

计算，令其导数为 0 ，

$${\nabla }_{{\mathbf{u}}_{T-1}}Q\left({\mathbf{x}}_{T-1},{\mathbf{u}}_{T-1}\right)={\mathbf{Q}}_{{\mathbf{u}}_{T-1},{\mathbf{x}}_{T-1}}{\mathbf{x}}_{T-1}+{\mathbf{Q}}_{{\mathbf{u}}_{T-1},{\mathbf{u}}_{T-1}}{\mathbf{u}}_{T-1}+{\mathbf{q}}_{{\mathbf{u}}_{T-1}}^T=0$$

得到：

$${\mathbf{u}}_{T-1}={\mathbf{K}}_{T-1}{\mathbf{x}}_{T-1}+{\mathbf{k}}_{T-1}$$

其中：

\begin{array}{l} \mathbf{K}_{T-1}=-\mathbf{Q}_{\mathbf{u}_{T-1}, \mathbf{u}_{T-1}}^{-1} \mathbf{Q}_{\mathbf{u}_{T-1}, \mathbf{x}_{T-1}} \\ \mathbf{k}_{T-1}=-\mathbf{Q}_{\mathbf{u}_{T-1}, \mathbf{u}_{T-1}}^{-1} \mathbf{q}_{\mathbf{u}_{T-1}} \end{array}

通过上面的分析，我们可以得到 LQR 算法中反向传播部分的算法：


反向传播计算出 k 之后，正向传播就简单了：