Latent Model

模型学习的好坏还与环境的复杂性有关。有些环境是部分可观测的，状态是高维的且存在较多冗余信息。 这节将考虑如何从结构设计的角度使得模型的学习变得简单容易。 我们需要考虑训练的模型有：

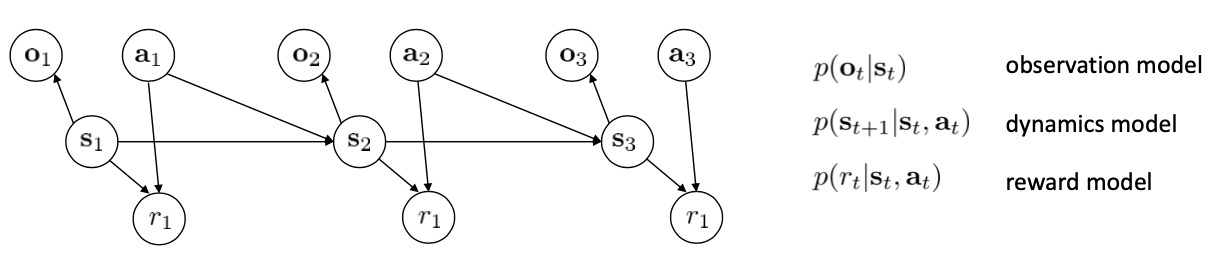
在全部可观测模型中，我们通常做的是对网络的输出做最大似然化： $$ \max _{\phi} \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} \log p_{\phi}\left(\mathbf{s}_{t+1, i} \mid \mathbf{s}_{t, i}, \mathbf{a}_{t, i}\right) $$ 但现在我们没有 $s_t$ ，只能对其期望做最大似然化： $$ \text { latent space model: } \max _{\phi} \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} E\left[\log p_{\phi}\left(\mathbf{s}_{t+1, i} \mid \mathbf{s}_{t, i}, \mathbf{a}_{t, i}\right)+\log p_{\phi}\left(\mathbf{o}_{t, i} \mid \mathbf{s}_{t, i}\right)\right] $$ 其中， $$ \text { expectation w.r.t. }\left(\mathbf{s}_{t}, \mathbf{s}_{t+1}\right) \sim p\left(\mathbf{s}_{t}, \mathbf{s}_{t+1} \mid \mathbf{o}_{1: T}, \mathbf{a}_{1: T}\right) $$ 这个分布需要这么复杂吗？

这里我们使用简单的方法，使用： $$ \text { expectation w.r.t. } \mathbf{s}_{t} \sim q_{\psi}\left(\mathbf{s}_{t} \mid \mathbf{o}_{t}\right), \mathbf{s}_{t+1} \sim q_{\psi}\left(\mathbf{s}_{t+1} \mid \mathbf{o}_{t+1}\right) $$ 为了简化讨论，这里的 observation model 是确定性的， $$ q_{\psi}\left(\mathbf{s}_{t} \mid \mathbf{o}_{t}\right)=\delta\left(\mathbf{s}_{t}=g_{\psi}\left(\mathbf{o}_{t}\right)\right) \Rightarrow \mathbf{s}_{t}=g_{\psi}\left(\mathbf{o}_{t}\right) $$ 我们的目标函数也就转换为： $$ \max _{\phi, \psi} \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} \log p_{\phi}\left(g_{\psi}\left(\mathbf{o}_{t+1, i}\right) \mid g_{\psi}\left(\mathbf{o}_{t, i}\right), \mathbf{a}_{t, i}\right)+\log p_{\phi}\left(\mathbf{o}_{t, i} \mid g_{\psi}\left(\mathbf{o}_{t, i}\right)\right) $$ 最后，在目标函数中加入关于奖励函数的优化： $$ \max _{\phi, \psi} \frac{1}{N} \sum_{i=1}^{N} \sum_{t=1}^{T} \log p_{\phi}\left(g_{\psi}\left(\mathbf{o}_{t+1, i}\right) \mid g_{\psi}\left(\mathbf{o}_{t, i}\right), \mathbf{a}_{t, i}\right)+\log p_{\phi}\left(\mathbf{o}_{t, i} \mid g_{\psi}\left(\mathbf{o}_{t, i}\right)\right)+\log p_{\phi}\left(r_{t, i} \mid g_{\psi}\left(\mathbf{o}_{t, i}\right)\right) $$ 整理一下，得到算法：