Linear Regression

假设目前输入变量只有两维，使用线性回归去预测时，线性方程为： $$ h_{\theta}(x)=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2} $$ 多添加一维输入 $x_{0}=1$ 可以化简线性方程为： $$ h(x)=\sum_{i=0}^{d}\theta_{i}x_{i}=\theta^{T}x $$

在给定训练集之后，如何去训练来得到线性方程的参数 $\theta$ 呢？ 最直接的方法就是让预测函数的结果与真实值越接近越好。 由此，可以定义损失函数（cost function）： $$ J(\theta)=\frac{1}{2}\sum_{i=1}^{n}(h_{\theta}(x^{i})-y^{i})^2 $$ 那么，我们的目标就转换成了让损失函数的值越小越好。

有了损失函数之后，我们可以# 梯度下降法 （gradient decent）去更新参数 $\theta$ ，最后 $\theta$ 可以收敛。 $$ \theta_{j}:=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}} J(\theta) $$ 对损失函数求导得：

\begin{aligned} \frac{\partial}{\partial \theta_{j}} J(\theta) &=\frac{\partial}{\partial \theta_{j}} \frac{1}{2}\left(h_{\theta}(x)-y\right)^{2} \\ &=2 \cdot \frac{1}{2}\left(h_{\theta}(x)-y\right) \cdot \frac{\partial}{\partial \theta_{j}}\left(h_{\theta}(x)-y\right) \\ &=\left(h_{\theta}(x)-y\right) \cdot \frac{\partial}{\partial \theta_{j}}\left(\sum_{i=0}^{d} \theta_{i} x_{i}-y\right) \\ &=\left(h_{\theta}(x)-y\right) x_{j} \end{aligned}

我们得到了更新 $\theta$ 的方法： $$ \theta_{j}:=\theta_{j}+\alpha\left(y^{(i)}-h_{\theta}\left(x^{(i)}\right)\right) x_{j}^{(i)} $$

这个更新方法我们称为 LMS。

给定数据集之后，我们如何利用数据集去更新参数呢？

这里由两种方法，一种是批次更新（batch gradient decent），一种是随机更新（stochastic gradient decent）。 批次更新法为：

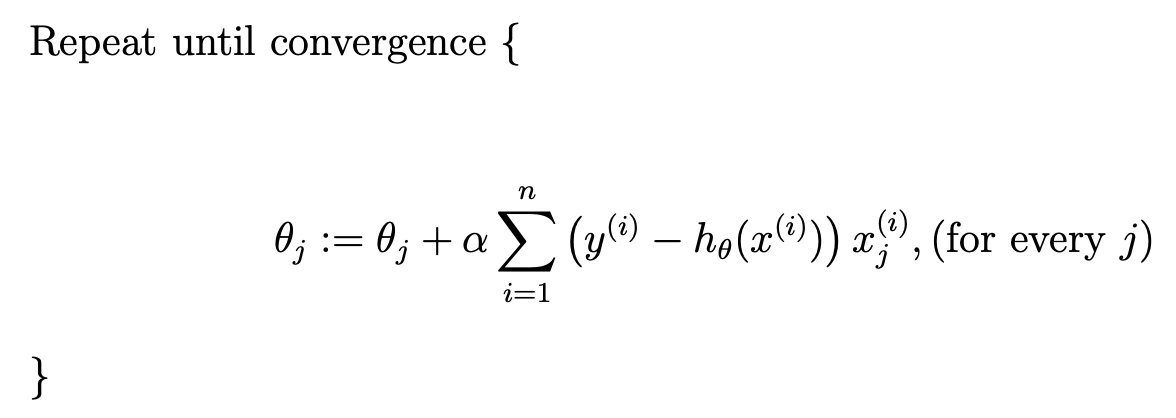
随机更新法为：

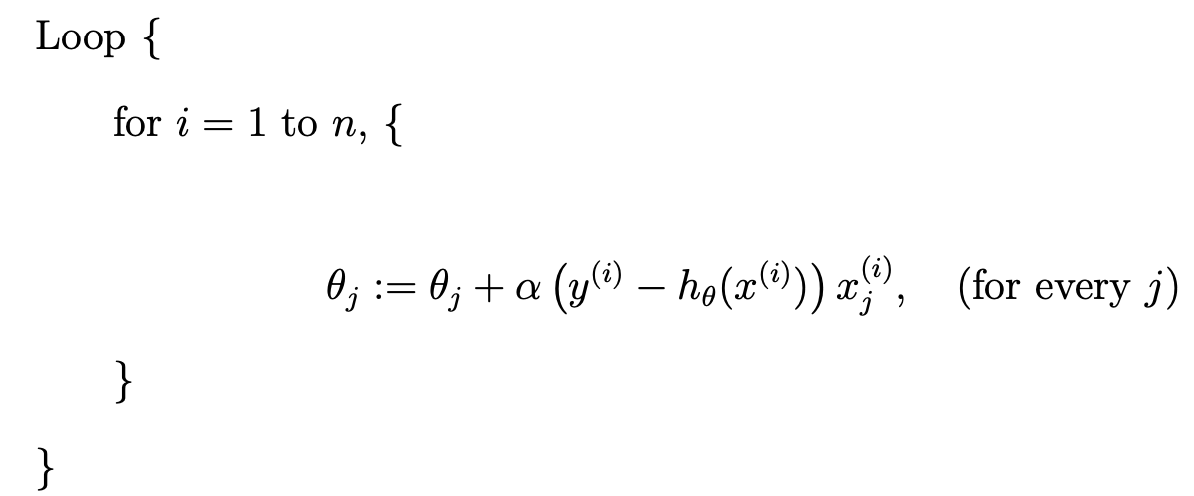
随机更新法要比批次更新更快收敛，因此一般推荐使用随机更新法。

上诉推导都是在一维输入的情况下，如果特征值存在多维，那么结果是否会不同呢？ 这里给出一般情况下更新方法的推导。 同理，给定训练集的输入为： $$ X=\left[\begin{array}{c} -\left(x^{(1)}\right)^{T}- \\ -\left(x^{(2)}\right)^{T}- \\ \vdots \\ -\left(x^{(n)}\right)^{T}- \end{array}\right] $$ 输出为： $$ \vec{y}=\left[\begin{array}{c} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(n)} \end{array}\right] $$ 损失函数为：

\begin{aligned} \frac{1}{2}(X \theta-\vec{y})^{T}(X \theta-\vec{y}) &=\frac{1}{2} \sum_{i=1}^{n}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} \\ &=J(\theta) \end{aligned}

损失求导结果为：

\begin{aligned} \nabla_{\theta} J(\theta) &=\nabla_{\theta} \frac{1}{2}(X \theta-\vec{y})^{T}(X \theta-\vec{y}) \\ &=\frac{1}{2} \nabla_{\theta}\left((X \theta)^{T} X \theta-(X \theta)^{T} \vec{y}-\vec{y}^{T}(X \theta)+\vec{y}^{T} \vec{y}\right) \\ &=\frac{1}{2} \nabla_{\theta}\left(\theta^{T}\left(X^{T} X\right) \theta-\vec{y}^{T}(X \theta)-\vec{y}^{T}(X \theta)\right) \\ &=\frac{1}{2} \nabla_{\theta}\left(\theta^{T}\left(X^{T} X\right) \theta-2\left(X^{T} \vec{y}\right)^{T} \theta\right) \\ &=\frac{1}{2}\left(2 X^{T} X \theta-2 X^{T} \vec{y}\right) \\ &=X^{T} X \theta-X^{T} \vec{y} \end{aligned}

推导过程中用到的公式： $a^{T}b=b^{T}a$ 当 $shape(a) = shape(b)$ ， $\nabla_{x}b^{T}x=b$ ， $\nabla_{x}x^{T}Ax=2Ax$

$\theta$ 的更新方法为： $$ \theta=\left(X^{T} X\right)^{-1} X^{T} \vec{y}^{3} $$

那么为什么要使用最小二乘作为损失函数呢？ 除了我们直观的理解：让预测函数和真实值越接近越好之外，能不能从概率的角度推导出来呢？

设真实值和输入之间存在如下关系： $$ y^{i}=\theta^{T}x^{i}+\epsilon^{i} $$ 其中， $\epsilon^{i}\sim\mathcal{N}(0,\sigma^{2})$ ，即： $$ p(\epsilon^{i})=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(\epsilon^{i})^2}{2\sigma^2}) $$ 那么： $$ p\left(y^{(i)} \mid x^{(i)} ; \theta\right)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}}{2 \sigma^{2}}\right) $$ 我们希望寻找一组参数 $\theta$ ，使得在给定输入 $x^{i}$ 的条件下，输出 $y^{i}$ 的概率最大。

可以使用# 最大似然法解决这个问题：

\begin{aligned} L(\theta) &=L(\theta;X,\vec{y})=p(\vec{y}|X;\theta) \\ &=\prod_{i=1}^{n} p\left(y^{(i)} \mid x^{(i)} ; \theta\right) \\ &=\prod_{i=1}^{n} \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}}{2 \sigma^{2}}\right) \end{aligned}

化简得：

\begin{aligned} \ell(\theta) &=\log L(\theta) \\ &=\log \prod_{i=1}^{n} \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}}{2 \sigma^{2}}\right) \\ &=\sum_{i=1}^{n} \log \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2}}{2 \sigma^{2}}\right) \\ &=n \log \frac{1}{\sqrt{2 \pi} \sigma}-\frac{1}{\sigma^{2}} \cdot \frac{1}{2} \sum_{i=1}^{n}\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2} \end{aligned}

因此，我们得到了最小二乘相同的损失函数： $$ \frac{1}{2} \sum_{i=1}^{n}\left(y^{(i)}-\theta^{T} x^{(i)}\right)^{2} $$

为了防止参数过大，出现过拟合的现象，我们在之前的损失函数中加入对参数的正则化惩罚。 惩罚有一般有两种：一范数和二范数。常用的是二范数。

此时的损失函数为； $$ \mathcal{L}(\theta) = ||\theta^{T}X-Y||_{2} + ||\theta^{T}\theta||_{2} $$ 对 $\theta$ 求导之后，可以直接令导数为 0 计算出 $\theta$ 或者使用梯度下降法求解。

\begin{aligned} P(\theta|Y) &= \frac{P(Y|\theta)P(\theta)}{P(Y)} \\ &= P(Y|\theta)P(\theta) \end{aligned}

假设 $$ P(\xi) \sim \mathcal{N}(0,\sigma_{1}^2) $$ $$ P(Y|\theta) \sim \mathcal{N}(X\theta, \sigma_{1}^{2}) $$ $$ P(\theta) \sim \mathcal{N}(0, \sigma_{2}^{2}) $$

对 $P(\theta|Y)$ 求其极大似然估计也可以得到和上诉类似的梯度更新方式。

前面讲的去预测某个输入 $x$ 的输出，通用的流程是：

1. 求使得 $\sum_{i}(y^{(i)}-\theta^{T}x^{(i)})^2$ 最小的参数 $\theta$
2. 输出 $\theta^{T}x$ 作为预测值

而 LWR 的思想却是：

1. 求使得 $\sum_{i}w^{(i)}(y^{(i)}-\theta^{T}x^{(i)})^2$ 最小的参数 $\theta$
2. 输出 $\theta^{T}x$ 作为预测值

$w^{(i)}$ 的取值为： $$ w^{(i)}=\exp\left( -\frac{(x^{(i)}-x)^2}{2\tau^{2}} \right) $$

如果 $w^{(i)}$ 很大，那么需要费很大劲去减小损失； 反之，如果 $w^{(i)}$ 很小，那么几乎可以不去考虑损失。

其实想想这样做也很合理。与输入的距离越近，对输出的结果影响越大，所以对应的权重需要加大，反之，亦然。

这种方法是# Non-parametric algorithm。 在进行预测的时候，需要使用训练集的数据。而之前训练好参数直接对数据进行预测的方法称为# Parametric algorithm。