Gradient

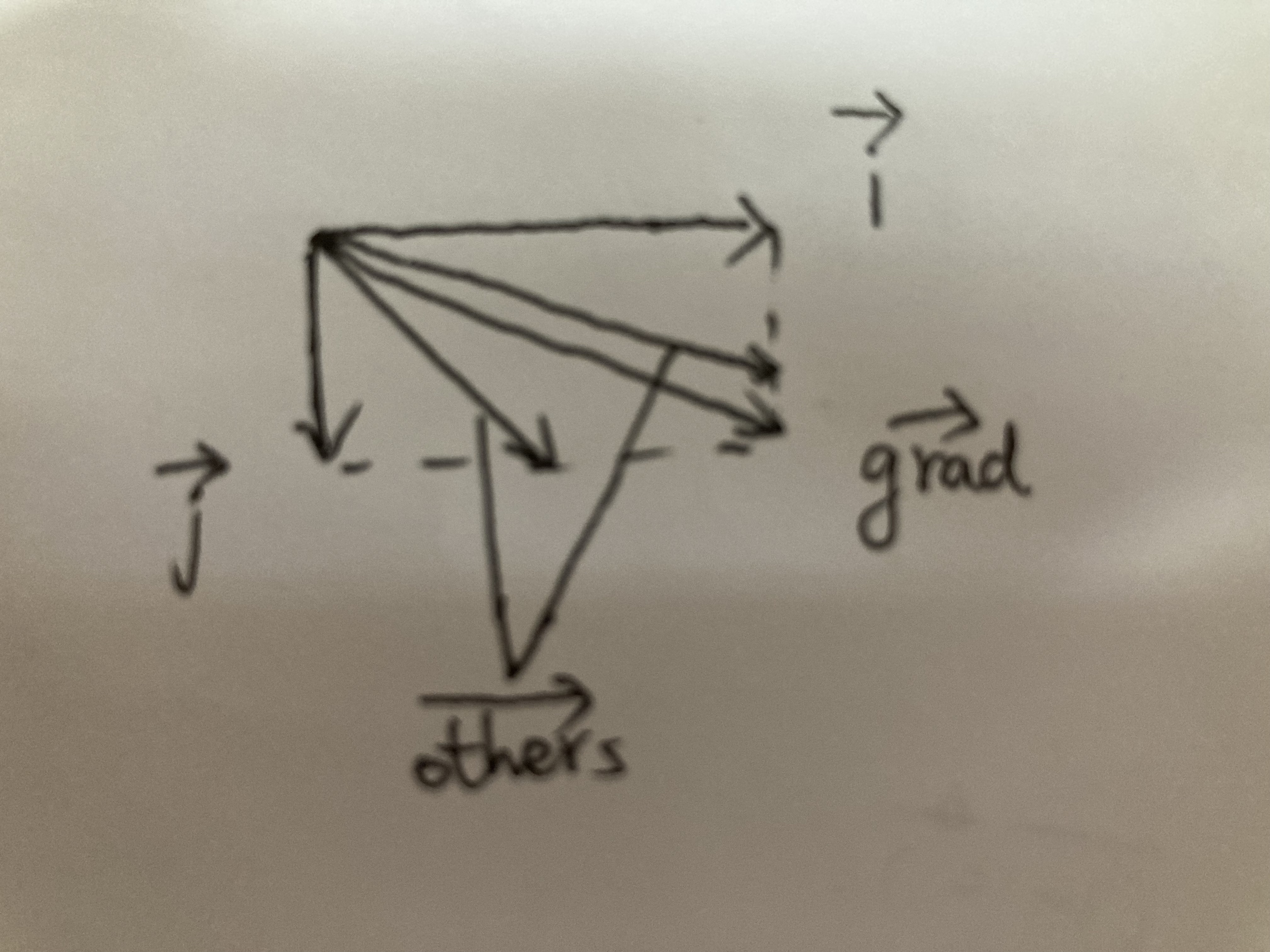
在二元函数的情形中，设函数 $f(x,y)$ 在平面区域 $D$ 内具有一阶连续偏导数， 则对于每一点 $P_{0}(x_0,y_0)\in D$ ，都可定出一个向量：

$$ f_{x}(x_0,y_0)\mathbf{i}+f_{y}(x_0,y_0)\mathbf{j} $$

这向量称为函数 $f(x,y)$ 在点 $P_{0}(x_0,y_0)$ 的梯度，记作 $\mathbf{grad}f(x_0,y_0)$ 或 $\nabla f(x_0,y_0)$ 。

梯度的方向是函数在这点的方向导数取得最大值的方向，它的模就是方向导数的最大值。