Reward Shaping

Often, a very simple pattern of extra rewards suffices to render straightforward an otherwise completely intractable problem.

Current Problems

Consider the following example of bugs that can arise:

In a system that learns to ride a simulated bicycle to a particular location. To speed up learning, they provided positive rewards whenever the agent made progress towards the goal. Because no penalty was incurred for riding away from the goal.

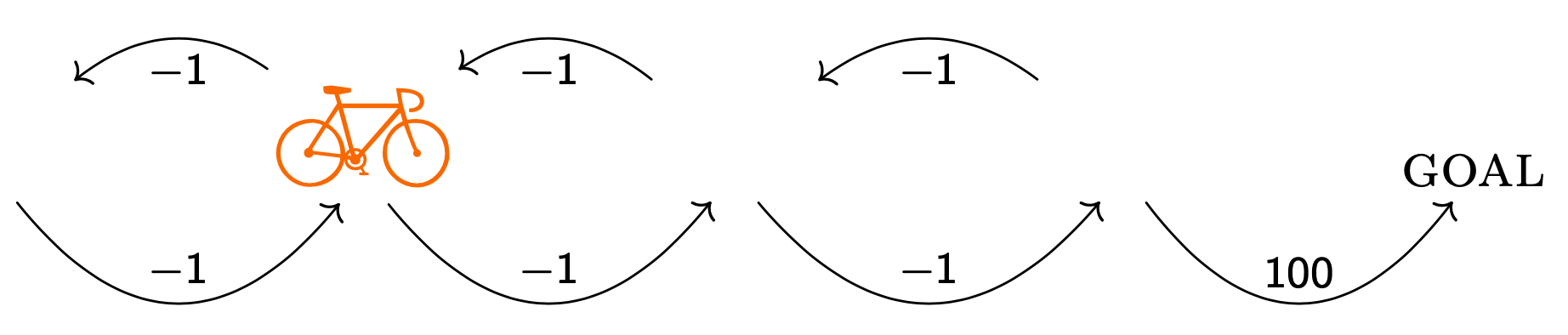
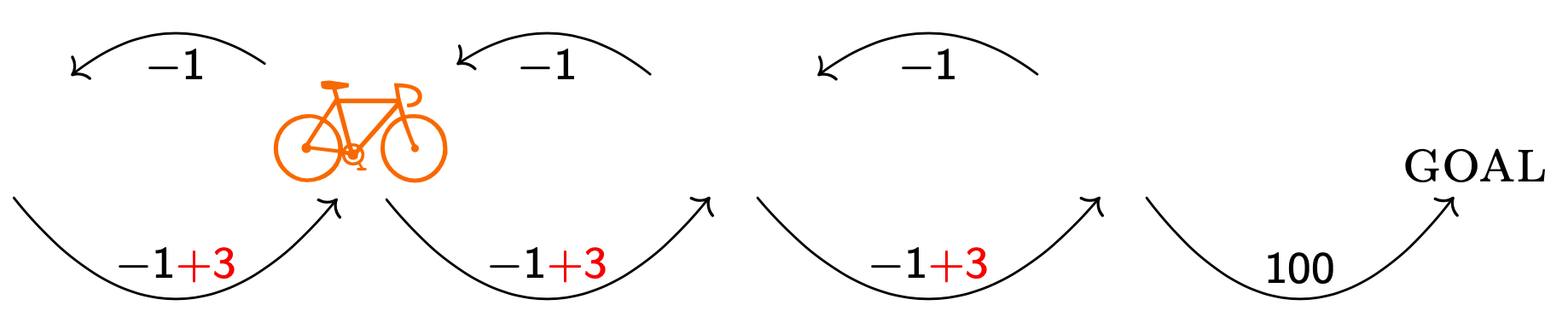
Hence it's now better for the bicycle to try to go in a cycle than to go to the goal.

A finite-state Markov decision process(MDP) is a tuple $M=(S,A,T,\gamma,R)$, where:

• $S$ is a set of states;
• $A=\{a_1,\dots,a_k\}$ is a set of actions;
• $T=\{P_{sa}(\cdot|s \in S,a \in A)\}$ is the next state transition probability;
• $\gamma$ is the discount factor;
• $R: S \times A \times S \rightarrow R$ is a bounded real function called the reward function.

A policy over a set of states S is a function $\pi: S \rightarrow A$.

Thus,

• Value function $V^{\pi}_{M}(s)=\mathbb{E}[R_1+\gamma R_2 + \cdots]$
• Action function $Q^{\pi}_{M}(s,a)=\mathbb{E}_{s^{\prime\sim P_{sa}}}[R(s,a,s^{\prime})+\gamma V^{\pi}_{M}(s^{\prime})]$

Hence, the optimal value function is $$ V^{*}_{M}(s) = \sup_{\pi}V^{\pi}_{M}(s) $$ The optimal Q-function is $$ Q^{*}_{M}(s,a) = \sup_{\pi}Q^{\pi}_{M}(s,a) $$ The optimal policy is $$ \pi^{*}_{M}(s) = \arg\max_{a\in A}Q^{*}_{M}(s,a) $$

We will run on a transformed MDP $M^{\prime}=(S,A,T,\gamma,R^{\prime})$ where $R^{\prime}=R+F$, and $F:S \times A \times S \rightarrow \mathbb{R}$ is also a bounded real-value function called the shaping reward function.

We are trying to learn a policy for some MDP M, and we wish to help our learning algorithm by giving it additional shaping rewards which will hopefully guide it towards learning a good policy faster.

But for what forms of shaping-rewards $F$ can we guarantee that $\pi_{M^{\prime}}^{*}$, the optimal policy in $M^{\prime}$ will also be optimal in $M$?

Definition A shaping reward function $F$ is potential-based if there exists $\Phi:S\rightarrow \mathbb{R}$ s.t. $$ F(s,a,s^{\prime}) = \gamma\Phi(s^{\prime}) - \Phi(s) $$

If $F$ is a potential-based shaping function, then every optimal policy in $M^{\prime}$ will also be an optimal policy in $M$.

Proof omission.

This suggests that a way to define a good potential function might be to try to approximate $V^{*}_{M}(s)$.